Mo's Algorithmのイメージを視覚的に理解したい

はじめに

Mo's AlgorithmはABC242-GやABC293-Gで出題され、典型アルゴリズムとなりつつあります。
一度理解すれば納得しやすいアルゴリズムなのですが、初めて学習したときに巷の図では個人的に分かりにくかったのでブログ内で整理してみました。

Mo's Algorithmのざっくりイメージ

例えば下図のように、 $0 \le L \le R \lt N$ となる $(L, R)$ が $Q$ クエリ与えられたとします。
(以下、図中では $N = Q = 200$ としています。横軸が $N$ です。)

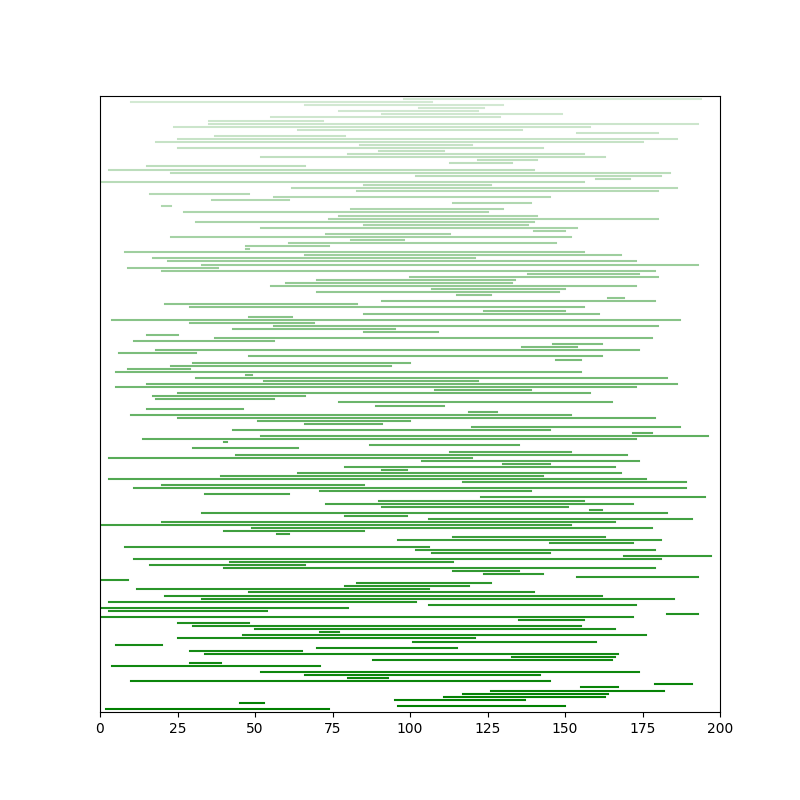
ここで、ブロックでクエリをグルーピングします。
$N$ を $\sqrt{Q}$ 分割し、ブロック長 $\lceil \frac{N}{\sqrt{Q}}\rceil$ ごと*1に $L$ が属するブロックにクエリをまとめます。*2

ブロックの中のクエリは、 $R$ でソートしておきます。
ここで昇順、降順、昇順……と交互にソートすると計算量的に有利です。

こうして並び替えたクエリについて上からシミュレーションして解いていきます。
範囲を1伸縮するのにかかる計算量を $O(1)$ とすると、計算量は以下の通りとなります。

$L$ に注目すると1クエリで最大 $\frac{N}{\sqrt{Q}}$ 変化するため、最悪計算量 $O(\frac{N}{\sqrt{Q}})$ $\times$ $Q$ クエリ $=$ $O(N \sqrt{Q})$
$R$ に注目すると1ブロックで最大 $N$ 変化するため、最悪計算量 $O(N)$ $\times$ $\sqrt{Q}$ ブロック $=$ $O(N \sqrt{Q})$
$Q$ クエリのソートに $O(Q \log{Q})$
よって全体の計算量 $O(N \sqrt{Q}+Q \log{Q})$

となるアルゴリズムでした。クエリ先読み+平方分割の合わせ技ですね。このようなテクニックはクエリ平方分割と言われているらしいです。

Mo's Algorithmが使える条件

$O(N \sqrt{Q})$ が間に合う条件である*3
区間伸縮の計算が $O(1)$ またはそれに近い
クエリがオフラインで与えられる(先読みができる)
配列の要素が不変である

例題

atcoder.jp

クエリは上記の仕組みでソートしておきます。
範囲を1伸ばすとき、もともと範囲内にある色のうち伸ばした部分の色と一致する個数が奇数の場合、組めるペアが増加するため答えが1増加します。
逆に範囲を1縮めるとき、縮めた部分の色と縮めた後の部分の色で一致する個数が偶数の場合、答えが1減少します。
よって範囲内の色を配列やハッシュセットで管理すれば $O(1)$ で区間を伸縮でき、合計 $O(N \sqrt{Q})$ で答えを出すことができます。

def resolve():
    def add(i):
        nonlocal nowans
        if d[i] % 2:
            nowans += 1
        d[i] += 1

    def rem(i):
        nonlocal nowans
        if not d[i] % 2:
            nowans -= 1
        d[i] -= 1

    import sys

    input = sys.stdin.readline
    n = int(input())
    a = tuple(map(int, input().split()))
    q = int(input())
    block_range = int(n / q**0.5) + 1
    qs = [[] for _ in range(n // block_range + 1)]
    for i in range(q):
        l, r = map(lambda x: int(x) - 1, input().split())
        qs[l // block_range].append((r, l, i))
    ans = [0] * q
    nowans = 0
    d = [0] * (n + 1)
    x = 0
    y = 0
    for index, qb in enumerate(qs):
        for r, l, i in sorted(qb, reverse=index % 2, key=lambda x: x[0]):
            while y <= r:
                add(a[y])
                y += 1
            while x > l:
                x -= 1
                add(a[x])
            while y > r + 1:
                y -= 1
                rem(a[y])
            while x < l:
                rem(a[x])
                x += 1
            ans[i] = nowans
    print(*ans, sep="\n")


if __name__ == "__main__":
    resolve()

Pythonのソートは遅いので、lが属するブロックごとにバケットソートの感覚で配列に入れ、ブロックごとにソートするのがポイントです。
またkey=lambda x: x[0]と指定してあげると高速になります(参考)。

テンプレート化しておくと使い回しが効きやすいアルゴリズムです。

github.com

おまけ

ABC174-FのMo's Algorithm解法をPythonで通そうとするとかなり厳しいです。*4
また区間伸縮に $O(\log{N})$ がかかる場合などももろに影響が出そうです。
Pythonにはちょっとだけ不利なアルゴリズムかもしれません。

あと改めて図を作ってみて、クエリが一様に分布しているとわかっている場合はブロック長の取り方を工夫したりできるのかな？と感じたりしました。

追記

言語アップデートで通るようになりました。
ただしrandom06は相変わらず強敵だったのでtupleをintに変換したりFastioを拝借したりと定数倍高速化は必要でした。

atcoder.jp

追記(ヒルベルト曲線)

ヒルベルト曲線の通りがけ順でソートすると定数倍軽くなるという記述も見かけたのでプロットしてみました。

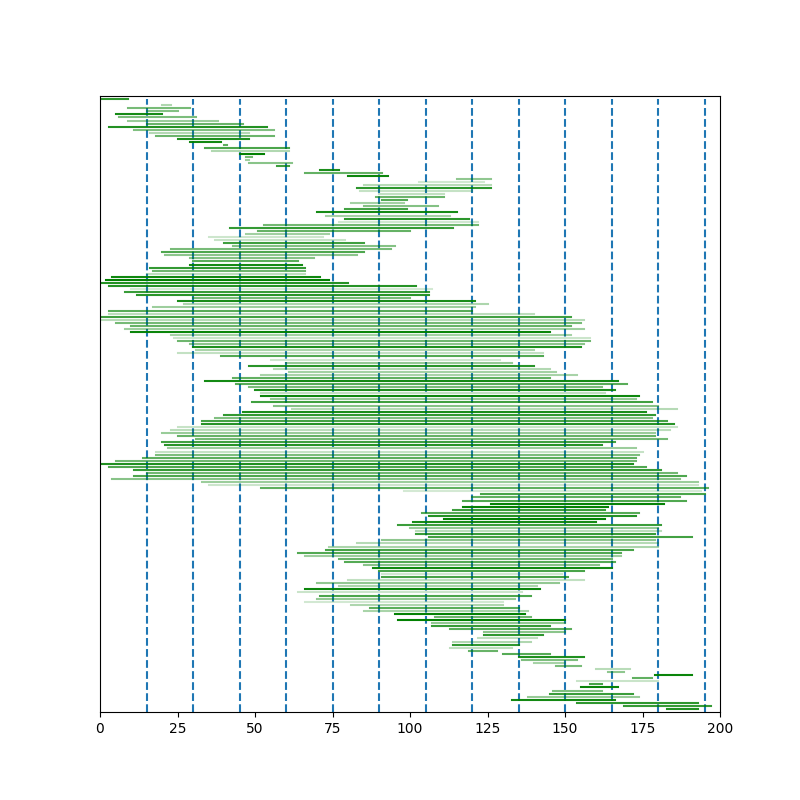
これを見ると悪くなさそうな遷移に見えます。
行けそうな気がしたので先駆者の記事を参考にして雑に解いてみたら逆に2倍近くかかってしまいました。
実験してみるとソート部分で2000msほどかかっていたのでPyPy3のソートが遅いのが原因っぽいてす。
バケットソートを挟むなど工夫するか、おとなしく言語アップデートを待ちましょう。~~またはPythonを使うのをやめましょう。~~

atcoder.jp

*1:実装上は簡単のため切り捨てて1を加算するとよい

*2:ブロック長は $\frac {\sqrt{3}N}{\sqrt{2Q}}$ が速いという記事もありますが速度はほぼ変わらず、好きな方で良いと思います